What Does
Shear Strain Mean?
Shear strain is the ratio of displacement to an object’s original dimensions due to stress, and is the amount of deformation perpendicular to a given line rather than parallel to it.
In engineering, shear strain is the tangent of the angle, and is equal to the length of deformation at its maximum divided by the perpendicular length in the plane of force application, which sometimes makes it easier to calculate.
Shear strain measures how much a given deformation differs from a rigid deformation. Shear strain is strain that results from the use of opposing forces in a parallel direction to the surface of an object. It is an angular change at some point in a shape.
Shear strain is the amount of contortion caused by the sliding of plane layers over each other within a deformity that can be applied by elongation, shortening, volume changes or angular distortion.
Shear strain can accelerate an object’s corrosion rate.
Corrosionpedia Explains Shear Strain
Shear strain is the strain resulting from the application of opposing forces in a direction parallel to a surface or to a planar cross section of a body. It is an angular change at some point in a shape.
For example, when scissors cut paper, they cause the paper to undergo a shear strain so large that the paper yields, coming apart where it is strained.
Strain is a normalized measure of deformation representing the displacement between the particles of an object relative to a reference length. Like stress, it may be classified as normal strain and shear strain.
An object that undergoes shear stress is one that experiences a tangent of an angle through which two adjacent sides rotate relative to an initial position. Shear strain measures changes in angles with respect to two specific directions.
Shear strain is the relative displacement in ratio of any perpendicular layer distance from a fixed layer. Any angular changes resulting between any mutually perpendicular planes is known as shear strain.
Shear strain can be calculated by the formula:
Shear Strain (γ ) = tan Φ
Where:
γ = shear strain (which does not have a unit)
τ = shear stress (unit of force over unit of area: N/m2 or pounds per square inch (psi) in the British Imperial System)
Other useful formulas:
G = shear modulus (defined as the ratio of shear stress over shear strain)
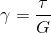
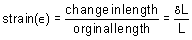
Strain is the measure of deformation of the material and is a non-dimensional quantity. It has no units and is simply a ratio of two quantities bearing the same unit.
Tensile strains are positive while compressive strains are negative. In shear strain, the shear stress acts along a surface. The stress produces deformation of the object, which is considered the distortion produced by shear stress on an element or rectangular block.
This shear strain or slide can be defined as the change at a right angle or the angle of deformation. Shear strain is measured in radians and hence has no units.
Shear strain has a relationship to shear modulus, which has elasticity coefficiency of a given substance that expresses the ratio between force per unit area (shearing stress) that deforms the substance and the shear produced by this force.