What Does
Tensile Modulus Mean?
The tensile modulus of a solid material is a mechanical property that measures its stiffness. It is defined as the ratio of its tensile stress (force per unit area) to its strain (relative deformation) when undergoing elastic deformation. This property has units similar to pressure, that is, Pa (N/mm2), psi, etc.
The tensile modulus is useful for evaluating how stiff a material is. In other words, how much the material is expected to deform (elastically) when subjected to a particular load. The higher a material’s tensile modulus is, the more force is required to deform it.
Based on the description above, the tensile modulus of a material can be expressed mathematically as:
E = σ / ε
Where:
ε = The tensile strain in the material (extension/original length)
σ = The tensile stress in the material
E = Tensile modulus (also known as the Young’s modulus)
Corrosionpedia Explains Tensile Modulus
In addition to being calculated using the above formula, the tensile modulus of a material may be determined graphically by measuring the slope of the linear portion of a typical stress-strain curve. In other words, it is the change in stress divided by the corresponding change in strain.
Different materials have very different tensile modulus values. For example, rubber has a tensile modulus of 1 MPa, while iron has a tensile modulus of 200 GPa. Therefore, iron is 200,000 times stiffer than rubber when subjected to tensile loading. Or, for a sample with similar geometrical properties, rubber will extend 200,000 times more than iron when subjected to the same load.
How Tensile Modulus is Determined
The tensile modulus of a material can be determined by conducting a tensile test, also known as a tension test. During this test, a test specimen, typically cylindrical in shape, is put into an apparatus where it is clamped at either end. A tensile axial load (or pulling force) is applied to one end of the specimen, while the other remains stationary. This gradually elongates or stretches the specimen at a standard rate until it ruptures.

Figure 1. A tensile testing machine. (Source: Ryzhov Sergey/Dreamstime.com)
The force in the sample that resists the pulling force is recorded and its elongation is measured. The results are then plotted on a chart called a stress-strain graph. A typical stress-strain graph is shown in the figure below.
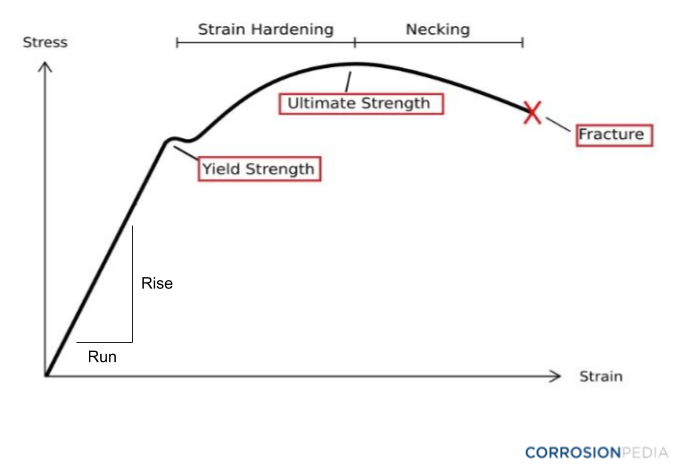
Figure 2. Typical stress-strain graph.
The straight-line portion (linear) area of the curve is known as the elastic zone. The gradient of this zone, i.e., the ratio of its rise to its run (change in stress/change in strain) is equal to the tensile modulus of the material.
Factors that Affect the Tensile Modulus of a Material
Any physical or mechanical property that affects a material’s stress or strain will ultimately affect the value of its tensile modulus. For example, the stress of an axially-loaded body is directly related to its cross-sectional area. Therefore, we can expect the tensile modulus of a specimen to relate to its size and shape. The bigger the area of an object is, the greater the number of intermolecular bonds present, thus, the higher the tensile stress needed to pull it apart.