Structural integrity is an extremely important aspect of any engineering endeavor for a multitude of reasons, not the least of which is safety and economic feasibility. Since these two factors are prime concerns in modern engineering, it is doubly important to understand the building blocks that make up this complex field.
To that point, the mechanical properties of construction material play a major role in determining how successful and long-lived your structure is going to be. Obviously, we’re not talking solely about designing and building said structure, but also about maintaining and repairing it.
If your trade, business or studies fall anywhere in that life cycle, then you should be familiar (and probably are) with this concept. However, we often overlook seemingly trivial but key ideas.
First is to understand the difference between the physical and the mechanical properties of a material. Second, terms like stress, strain and strength are often not completely clear, sometimes even among experts. (For further reading on these topics, see What is the Difference Between Strength and Toughness?)
So, a subset of the field of structural integrity is mechanical properties, and a subset of these properties is strength.
Before we can deal with what tensile strength really is, we will need to address some of those stated overarching issues. If you feel that you do not need this introduction just proceed straight to the third section of this article.
Mechanical Properties of Materials
Mechanical properties describe how a certain material reacts to and withstands applied forces, or to be more precise, loads, which are forces exerted on a particular body or a surface. When it comes to material behavior, we tend to separate these loads into several distinct types: compressive, tensile, impact, cyclical or fatigue loads, or loads at high temperature.
Obviously, mechanical properties are a subset of physical properties and the main difference is that the more general physical properties are not influenced by this type of external forces. The weight of a material is not influenced by the type and intensity of a load applied, it is a function of its mass and gravitational force.
Mechanical properties are influenced by the material on literally every length-scale of its structure. If we observe two pieces of seemingly identical alloy, say, Al 5083, we would expect them to have an identical composition. But, if we were to take a closer look we would see that in practice, this is not exactly the case.
Even if we used the same process of fabrication they would have slightly different grain sizes, different boundaries and inclusions. Even if they have the same concentration of the alloying elements, their distribution is not homogeneous and it would vary greatly in every single piece. And as we go further down the scale, we could as well see that even on the atomic level they wouldn’t be identical, because various crystal lattice defects, interstitial defects and substitutional atoms would be present in different amounts at different places.
In other words, we can’t predict with mathematical certainty the behavior of materials, and thus we are forced to use experimentation and estimates, albeit pretty accurate ones.
Stress, Strain, and Strength
While knowing how loads affect a material is important, we can gain a better understanding of what is actually happening with the engineered material if we introduce the concept of stress.
When a force acts on a material, it creates an internal force that tries to maintain the equilibrium of the system. It should be noted that these internal forces exist in the material already, even when not under load.
These internal forces are already present between the atoms, molecules and crystals that make up the material, so this new internal force that is introduced changes the vector and the intensity of the resultant internal force.
If we observe this resultant force over the area perpendicular to it, we get stress. Stress is an internal characteristic of the material that tells us how the internal force is spread out throughout the material.
Or, if we put into an equation, it would look something like this:
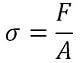
Where F is the acting force, A is area normal to that force vector (in engineering usually a cross-section) and σ is traditionally used as a symbol for stress.
This distribution of stress throughout the cross-section that is normal to the force vector isn’t uniform in the vicinity of the external forces, but luckily stress tends to “even out” if we observe it far enough from where the force is acting on the member (this is known as Saint Venan principle).
If we look at a material even in its unloaded state, chances are there are some residual stresses in it due to material imperfections and the fabrication and construction processes involved. Indeed, we even use this to our advantage, by pre-stressing the part in the opposite direction of the expected stress under load.
On the other hand, strain is a relative elongation of a material under load. This means that stress is an effect, and strain is a cause of said effect. Since strain represents relative elongation, it is a dimensionless number, unlike deformation, which we measure in typical length units (usually millimeters, centimeters or inches).
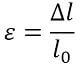
Strain, ε, is measured by taking the change in the specimen length, and dividing it by the original length l0.
Even though stress and strain are tied, their relationship depends on a number of factors that make it impossible to put into a simple mathematical relation. For that reason, we have developed stress-strain diagrams based on experimental data. Luckily, construction materials tend to behave similarly so there are only a few subsets of these diagrams that are important to us.
The strength of a material represents certain stress values of a material. Since we also have to take into account the effect of strain in the case of materials that deform prior to breaking, these two characteristics are key to understanding and estimating material strength.
In theory, every material would have consistent mechanical properties, but this isn’t entirely true in practice. Since these properties are tied to loads, and by extension stress in the material, how that stress is distributed is important, which is mainly dependent on the microstructure of the material. Since no engineering material is truly homogenous, different grain sizes, inclusions and other factors lead to varying stress distribution and local stress concentrations.
For example, two beams made of aluminum having the same chemical composition might have the same weight and melting point, which are physical properties, but they would have different real tensile strength due to differences in their microstructure. If one beam has a much larger grain size than the others, it would also have significantly lower tensile strength.
Not all mechanical properties are microstructure sensitive, though. For example, Young’s modulus (modulus of elasticity) can be considered the same for one material, no matter the microstructure.
Tensile Strength
Since stress is dependent on the surface area, this means that the loading capacity of the material is directly correlated to it also. In other words, thicker members can withstand higher static loads, which is a logical and intuitive conclusion.
But let’s put this every day, common knowledge under more intense scrutiny, and consider the implications:
A force of 100 N will always be the same, but a stress of 100 MPa (N/mm2) has an infinite number of combinations of force intensity and surface area that can fulfill the requirement. This is exactly the kind of thing that sets apart mechanical properties from physical.
Now, the ultimate strength of a material represents the amount of stress it can withstand prior to breaking. If we talk about ultimate tensile strength, that means that we are considering the maximum tensile stress it can sustain.
The tensile strength of a particular material is always the same (in theory) but the loads it can sustain depend on its dimensions and geometry (amount of stress and stress concentrations).
To complicate matters even further, we need to take into account the direction of the load because material behavior can vary greatly.
Compressive stress is similar in nature to tensile stress as it is produced by the same type of force but in an opposite direction. Generally, construction materials are less sensitive to compressive stresses, meaning that they have much higher compressive strength compared to tensile strength.
Being aware of this fact is important when we look at loads that tend to flex the material instead of stretching it.
If we consider a flexing load that, for example, bends an I-beam from the top side under a 90° angle, we can observe that the lower half of the beam is under compression and upper half is under tension. (For another example, read Tensile Time Bomb: How Overtapping Compromises Pressure Bolt Safety.)
Since the compressive strength of steels, aluminum and other common construction materials is much greater than their tensile strength, we are usually only concerned with the tensile portion of the member. Furthermore, we can introduce a concept of metal fibers, which would be imaginary thin strains of material that run length-wise.
In the case of flexure, we can see that the loads are not distributed evenly – outermost fibers are under the highest stress. This means, a bit counterintuitively, that the flexural strength of a material is often higher than the straight, uniaxial tensile strength.
Obviously, this example of a symmetric beam with a specific load has been taken for simplicity’s sake, since we would have to take into consideration uneven stress distribution and shear stresses in other cases.
Shear stress, impact and cyclic stress can be even more dangerous to the health of a structure, but talking about the effects of these mechanisms would go beyond the scope of this article.
Tensile Strength as a Factor in the Construction and Corrosion Industries
Knowing how stress is going to be distributed is one of the most important things in engineering design. If we can predict the type of load that the structure or part is going to be under, we can choose (or develop) an appropriate profile and size, which allows us to reduce weight and significantly cut costs, without affecting safety or functionality.
An I-beam cross-section is designed that way because outermost sections are under the highest stress, so we reduce it by increasing the surface. Conversely, since the middle part of the beam is under less stress (or same amount if it’s uniaxial where all fibers share the stress equally), we can reduce the amount of the material since it is effectively not doing anything – a potential failure would not start there.
Besides ultimate tensile strength, another important stress milestone is yield strength, which can be found in ductile materials. Yield strength is the maximum stress that a material can endure before it starts to plastically deform (before it retains the new shape even when the load is removed).
Not all materials have yield strength. For the most part, structural materials can be divided into two categories: ductile and brittle. Ductile materials are the ones that deform prior to breaking, and brittle materials simply crack and shatter. Obviously, yield strength as a concept applies only to ductile materials.
Simply put, tensile stress is caused by tensile forces. But we have to bear in mind that these forces can come from a multitude of sources. There can be residual stresses in materials introduced during the fabrication process or construction, as well as the stresses caused by the weight of the structure itself and the active loads it is sustaining.
Corrosion can have a major effect on tensile strength, as it can change the chemical composition of a material, potentially reducing strength in the process. (To learn more, read Effect of Corrosion on a Material’s Tensile Strength and Ductility.)
While that can happen, there are several more significant ways it can influence the load-bearing capacity of a structure. Corrosion can greatly reduce the effective cross-section or surface of an element that takes on the load, increasing the acting stress in that manner.
Furthermore, it can influence crack nucleation and propagation, and the combined effects of corrosion and static loads (stress corrosion cracking or SCC), or corrosion and dynamic loads (corrosion fatigue) are very dangerous damage mechanisms.
When one is designing any kind of structure, it is of paramount importance to take into account all of these factors – residual stresses, types of loads, tensile strength, working temperature and corrosion – to be certain that the structure will behave in a predictable manner, within safety margins, while being economically feasible. Likewise, having a basic knowledge of these concepts is important in maintenance, corrosion prevention and construction.
Testing Methodology and the Difference between Ductile and Brittle Materials
Testing is done by measuring the stress and corresponding strain of standardized test specimens. Typically, a unidirectional force is applied to a specimen, which we can measure directly from the machine that applies it (normalized through stress), and we measure the strain with a strain gauge or extensometer.
Ceramic and other brittle materials have a fairly straightforward Hookean relationship. As the stress increases, the strain increases proportionally until the breaking point, which we can consider as the tensile strength of such a material. Since there is no plastic deformation involved, brittle materials do not have yield strength, and their failure results in a clean, even break. However, since these materials tend to break when put into the grips of the tensile testing machine, bend tests are usually used to measure their tensile strength.
In ductile materials, we can observe several distinct differences that are not present in brittle materials. Steel, aluminum and other metallic materials tend to behave in a Hookean fashion until certain point is reached, after which several curious things happen.
These material start to plastically deform and, as it yields, the stress values remain the same even as we increase the force applied. When a material yields, the energy that was introduced into the system that would normally be seen as an increase in stress is spent on overcoming the discontinuities in the material that prevented deformation until that point.
This plastic deformation leads to a narrowing of the cross-section, known as necking, and after the yield phase is over, the reduced cross section means that the stress is spread over a smaller area, leading to rapid increase in strain up to a breaking point.
Although it would be logical to expect that the plastic deformation starts right where the linear portion of the stress-strain curve ends, there is a slight amount of non-linear strain that can be reset, due to molecular forces in the material. For that reason a good rule of thumb is that the yield point can be found at a cross-section of the curve and a line that runs parallel to the linear curve section, but is offset 0.2% on the strain ordinate.
The stress value at which this plastic deformation, or yielding begins, is known as the yield strength. If a material is subjected to stress that is lower than this point, all the deformation it experiences is elastic in nature, and it will return to its original shape when the load is removed.
After the yielding is over, it is followed by non-linear stress-strain growth.
In this last phase, we need to differentiate between true stress and engineered stress. Real stress increases in a non-linear fashion due to the rapidly diminishing cross section, while engineering stress uses the nominal, initial cross section of the specimen, meaning that the engineering curve stress seems to drop for a while as strain increases until the breaking point.
The peak stress on the engineering curve is the maximum stress, or ultimate tensile strength.
Since the tensile strength of a material depends on its chemical composition and microstructure, the values can vary greatly, as you can see Table 1:
| Material |
Yield Strength
(MPa) |
Ultimate Strength
(MPa) |
Density
(g/cm3) |
| Structural steel ASTM A36 steel |
250 |
400 |
7.8 |
| Mild steel 1090 |
248 |
841 |
7.58 |
| Human skin |
15 |
20 |
2.2 |
| 2800 Maraging steel |
2617 |
2693 |
8.0 |
| AISI 4130 Steel, water quenched 855°C (1,570°F), 480°C (900°F) temper |
951 |
1110 |
7.85 |
| Titanium 11 (Ti-6Al-2Sn-1.5Zr-1Mo-0.35Bi-0.1Si), Aged |
940 |
1040 |
4.5 |
| Steel, API 5L X65 |
448 |
531 |
7.8 |
| Steel, high strength alloy ASTM A514 |
690 |
760 |
7.8 |
| High-density polyethylene (HDPE) |
26-33 |
37 |
0.95 |
| Polypropylene |
12-43 |
19.7-80 |
0.91 |
| Stainless steel AISI 302 – Cold-rolled |
520 |
860 |
8.19 |
| Cast iron 4.5% C, ASTM-A-48 |
130 |
200 |
|
| “Liquidmetal” alloy |
1723 |
550-1600 |
6.1 |
| Beryllium 99.9% Be |
345 |
448 |
1.84 |
| Aluminum alloy 2014-T6 |
414 |
483 |
2.8 |
| Polyester resin (unreinforced) |
55 |
|
|
| Polyester and Chopped Strand Mat Laminate 30% E-glass |
100 |
|
|
| S-Glass Epoxy composite |
2358 |
|
|
| Aluminum alloy 6061-T6 |
241 |
300 |
2.7 |
| Copper 99.9% Cu |
70 |
220 |
8.92 |
| Cupronickel 10% Ni, 1.6% Fe, 1% Mn, balance Cu |
130 |
350 |
8.94 |
| Brass |
200+ |
550 |
|
| Tungsten |
|
1510 |
19.25 |
| Glass |
|
33 |
2.53 |
| E-Glass |
|
1500 for laminates,
3450 for fibers alone |
2.57 |
| S-Glass |
|
4710 |
2.48 |
| Basalt fiber |
|
4840 |
2.7 |
| Marble |
|
15 |
|
| Concrete |
|
3 |
2.7 |
| Carbon fiber |
|
1600 for laminate,
4137 for fiber alone |
1.75 |
| Carbon fiber (Toray T1000G) |
|
6370 fiber alone |
1.8 |
| Human hair |
|
380 |
|
| Bamboo |
|
350-500 |
0.4 |
| Spider silk |
|
1000 |
1.3 |
| Darwin’s bark spider silk |
1652 |
|
|
| Silkworm silk |
500 |
|
1.3 |
| Polybenzoxazole (Zylon) |
|
2700 |
1.56 |
| Pine wood (parallel to grain) |
|
40 |
|
| Bone (limb) |
104-121 |
130 |
1.6 |
| Nylon, type 6/6 |
45 |
75 |
1.15 |
| Epoxy adhesive |
|
12-30 |
|
| Rubber |
|
15 |
|
| Boron |
|
3100 |
2.46 |
| Silicon, monocrystalline (m-Si) |
|
7000 |
2.33 |
| Silicon carbide (SiC) |
|
3440 |
|
| Ultra-pure silica glass fiber-optic strands |
|
4100 |
|
| Sapphire (Al2O3) |
400 at 25°C
275 at 500°C
345 at 1000°C |
1900 |
3.9-4.1 |
| Boron Nitride Nanotube |
|
33000 |
|
| Diamond |
1600 |
2800 |
3.5 |
| Graphene |
|
130000 |
1.0 |
| First carbon nanotube ropes |
|
3600 |
1.3 |
| Colossal carbon tube |
|
7000 |
0.116 |
| Carbon nanotube |
|
11000-63000 |
0.037 – 1.34 |
| Carbon nanotube composites |
|
1200 |
|
| Iron (pure mono-crystal) |
|
3 |
7.874 |
Table 1. Typical tensile strengths of some materials.
It is important to note that for the considerations stated here we talked about static loads. In the case of dynamic or cyclic loads we need to approach the matter a bit differently and take into account impact, fatigue, and the corresponding mechanical properties – toughness and fatigue life – of the material.
Conclusion
The tensile strength of materials is one of the most important concepts in mechanical engineering and materials science, and its discovery has revolutionized the way we build things. While it is by no means a sure-fire way to guarantee the reliability and safety of a structure due to all the different issues mentioned here (and many more), it is an important guideline in dimensioning of various parts and members, and it helps us predict how a part will behave and the lifespan we can expect from a structure.